Bagi kamu yang mendalami ilmu statistik, mungkin kamu tidak akan merasa asing jika mendengar kata standar deviasi. Namun, bagi kamu yang belum begitu mengenal ilmu statistik, kata ini mungkin terdengar cukup asing di telinga.
Sebenarnya, standar deviasi itu apa dan apa pula fungsinya? Bagi kamu yang penasaran dan ingin memahaminya lebih jauh lagi, silahkan simak uraian di bawah ini!
DAFTAR ISI:
Pengertian Standar Deviasi
Definisi standar deviasi adalah suatu nilai statistik yang berguna untuk menentukan seberapa dekat titik data individu ke nilai rata-rata sampel (mean) serta persebaran datanya dalam sampel.
Standar deviasi dapat digunakan untuk menerangkan homogenitas kelompok dengan ketentuan yaitu:
- Jika standar deviasi sama dengan 0 (nol) maka nilai yang terdapat dalam kelompok himpunan tersebut adalah sama
- Jika standar deviasi lebih besar maka titik data yang dimiliki oleh individu jauh dari mean atau nilai rata-rata sampel
Cara pertama yang harus kita lakukan sebelum menghitung standar deviasi yaitu menghitung mean atau nilai rata-rata dari sampel. Untuk mencari rata-rata atau mean maka jumlahkanlah semua nilai data kemudian bagi dengan banyaknya data yang menjadi sampel.
Setelah Anda menemukan nilai rata-ratanya, maka langkah selanjutnya adalah menghitung besarnya penyimpangan setiap sampel dari nilai rata-rata atau biasa disebut varian. Sedangkan standar deviasi diperoleh dengan menghitung akar kuadrat dari varian.
Fungsi Standar Deviasi
Untuk mengetahui apakah titik data yang dijadikan sampel dapat mewakili seluruh populasi atau tidak, biasanya para ahli statistik akan menggunakan rumus standar deviasi.
Hal ini dikarenakan dalam suatu populasi, untuk mencari data yang tepat yang dapat mewakili seluruh populasi bukanlah sesuatu yang mudah. Standar deviasi akan memudahkan kita dalam menentukan data yang tepat untuk mewakili suatu populasi.
Misalnya, jika kita ingin mengetahui berapa berat badan rata-rata anak perempuan yang berusia 3 hingga 4 tahun, maka kita dapat mengambil sampel berat badan dari beberapa anak perempuan yang berusia 3 hingga 4 tahun kemudian mencari standar deviasi dan rata-ratanya.
Dari perhitungan yang telah kita lakukan maka kita akan memperoleh nilai berat badan yang tepat yang dapat mewakili seluruh populasi.
Cara Menghitung Standar Deviasi Secara Manual
Mengetahui rumus varian dan standar deviasi merupakan langkah pertama yang harus kita tempuh dalam menentukan nilai standar deviasi.
Rumus Varian yaitu:
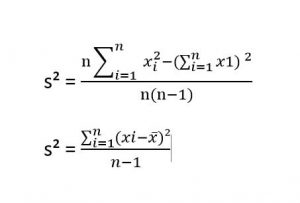
Rumus Standar Deviasi yaitu:
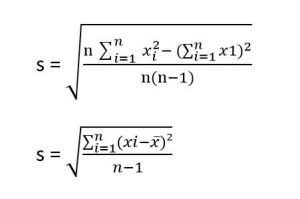
Keterangan:
- s² = Varian
- s = Standar Deviasi
- n = jumlah sampel
- x = rata-rata
- xi = nilai x ke i
Contoh Soal:
Berdasarkan sampel yang diambil terhadap tinggi siswa di suatu kelas diperoleh data sebagai berikut:
167, 180, 170, 169, 160, 175, 165, 173, 170, 172
Banyak sampel dari data di atas (n) adalah 10 sedangkan (n-1) = 9. Untuk mempermudah dalam penghitungan, Kamu dapat membuat tabel seperti di bawah ini:
| i | xi | xi² |
| 1 | 167 | 27889 |
| 2 | 180 | 32400 |
| 3 | 170 | 28900 |
| 4 | 169 | 28561 |
| 5 | 160 | 25600 |
| 6 | 175 | 30625 |
| 7 | 165 | 27225 |
| 8 | 173 | 29929 |
| 9 | 170 | 28900 |
| 10 | 172 | 29584 |
| Ʃ | 1701 | 289613 |
Selanjutnya kita mencari varian dengan cara:

Setelah mengetahui nilai varian sebesar 30,32 maka standar deviasi dapat diperoleh dengan mengakarkuadratkan nilai varian yaitu s = = 5,51. Jadi standar deviasi untuk data sampel di atas adalah 5,51.
Cara Menghitung Standar Deviasi Berkelompok
Selain untuk menghitung data yang bersifat tunggal, juga terdapat rumus varian dan standar deviasi untuk data kelompok yaitu:
Rumus Varian data kelompok:
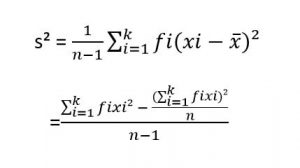
Rumus Standar Deviasi data kelompok:
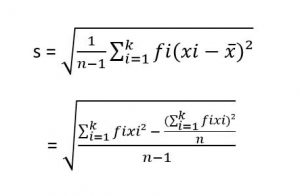
Contoh Soal:
Pada suatu penelitian terhadap tinggi badan siswa SMA Negeri 4 Bandung diperoleh data sebagai berikut:
| Tinggi Badan | Frekuensi (fi) |
| 151-155 | 3 |
| 156-160 | 4 |
| 161-165 | 4 |
| 166-170 | 5 |
| 171-175 | 3 |
| 176-180 | 2 |
Melalui data di atas, kita dapat mengetahui jika banyaknya data pada interval yaitu ( ). Untuk memudahkan dalam menghitung standar deviasi, kamu dapat membuat tabel seperti di bawah ini:
| xi | fi | (fixi ) |
( fixi)² |
| 153 | 3 | 459 | 70277 |
| 158 | 4 | 632 | 99856 |
| 163 | 4 | 652 | 106276 |
| 168 | 5 | 840 | 141120 |
| 173 | 3 | 519 | 89787 |
| 178 | 2 | 356 | 63368 |
| 21 | 3458 | 570634 |
Setelah membuat tabel di atas, kemudian kamu dapat menghitung varian dengan rumus seperti di bawah ini:
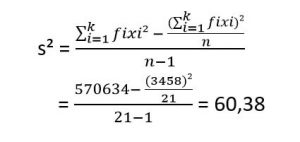
Berdasarkan penghitungan diperoleh nilai varian sebesar 60,83 dan untuk standar deviasi diperoleh dari akar kuadrat dari varian s = akar 60,83 = 7,8. Jadi, berdasarkan data kelompok di atas diperoleh standar deviasi sebesar 7,8.
Cara Menghitung Standar Deviasi dengan Kalkulator
Kamu dapat menghitung standar deviasi menggunakan kalkulator disamping dengan cara manual. Namun, Anda tidak dapat menggunakan kalkulator biasa untuk menghitungnya, Anda harus menggunakan kalkulator scientific.
Bagaimana jika Anda tidak memilikinya? Cara paling mudah yaitu dengan menggunakan kalkulator scientific online atau mendownload aplikasi kalkulator scientific di apps store.
Tahapan-tahapan menghitung standar deviasi menggunakan kalkulator:
- Nyalakan kalkulator dengan menekan tombol ON
- Kemudian tekan tombol MODE yang terletak di samping tombol ON yang berada di ujung kanan atas
- Tekan tombol nomor 3 (STAT) untuk memilih mode statistik
- Kemudian tekan tombol nomor 1 (VAR – 1)
- Masukkan sampel data yang ingin dihitung kemudian tekan tanda =, angka, = hingga semua sampel data habis. Jangan lupa selalu menekan tombol = ketika menginputkan data sampel.
- Lalu tekan tombol AC
- Kemudian tekan tombol SHIFT
- Tekan tombol 1 (STAT), 4 (VAR), 3 (σ x) untuk mengetahui hasil akhirnya
- Tekan tombol = sebagai langkah terakhir
Cara Menghitung Standar Deviasi di Excel
Bagi kamu yang mahir mengoperasikan program Microsoft Excel, kamu juga dapat memanfaatkannya untuk menghitung standar deviasi.
Cara yang satu ini terbilang mudah, karena Excel telah menyediakan rumus khusus untuk menghitung standar deviasi yaitu dengan menggunakan STDEV.
Untuk memudahkan kamu dalam mengaplikasikannya, silahkan simak contoh di bawah ini!
Contoh:
Data nilai mata pelajaran Bahasa Inggris siswa SMP Taruna Bangsa adalah sebagai berikut:
60, 80, 90, 70, 80, 95, 80
Tentukan standar deviasi dari data nilai mata pelajaran Bahasa Inggris tersebut!
Jawaban:
Masukkan data-data tersebut ke dalam tabel pada Microsoft Excel
| A | B | |
| 1 | A | 60 |
| 2 | B | 80 |
| 3 | C | 90 |
| 4 | D | 70 |
| 5 | E | 80 |
| 6 | F | 95 |
| 7 | G | 80 |
| STDEV | =STDEV(B1:B7) |
Saat kamu menekan tombol enter maka akan muncul nilai standar deviasi sebesar 11.70. Rumus tersebut berdasarkan sampel data yang terdapat pada kolom B1 hingga B7 jadi bukan merupakan rumus pasti.
Jika kamu ingin menghitung sampel data pada kolom C5 hingga C12 maka kamu tinggal mengganti B1:B5 dengan C2:C12. Cukup mudah bukan? Selamat mencoba.
Itulah beberapa uraian mengenai standar deviasi, fungsi dan contoh cara menghitungnya. Semoga bermanfaat.
Situs informasi dan edukasi Indonesia yang khusus menyajikan konten menarik dan segar seputar kedokteran, farmasi, dan kesehatan masyarakat.